Tutorial(japanese)

yaf2qは、量子化学計算で用いられるフェルミオン・量子ビット変換を実行するためのPythonライブラリです。以下に示す2つの機能を提供しています。

• フェルミオン・量子ビット変換の実行

  • フェルミオン・量子ビット変換の方法として従来からよく知られている「Jordan-Wigner変換」「Parity変換」「Bravyi-Kitaev変換」に対応するとともに、より汎用的にフェルミオン・量子ビット変換を記述できる「Ternary Tree（三分木）を用いた変換」にも対応しています。

• フェルミオン・量子ビット変換の最適化

  • Ternary Treeを用いてフェルミオン・量子ビット変換を実行したときに、量子ビット演算子に関する何らかの指標（例えば、ハミルトニアンの各項を構成するパウリ重みや、量子位相推定などの量子アルゴリズムを実行する量子回路の深さなど）が最小の値をとるような最適なTernary Treeの構造を探索することができます。

以下では、上記2つの機能をどのように実行するかを順に説明します。まず「フェルミオン・量子ビット変換の実行」についてです。

フェルミオン・量子ビット変換の実行

従来の変換法：Jordan-Wigner／Parity／Bravyi-Kitaev変換

フェルミオン・量子ビット変換を管理するF2QMapperクラスを以下のようにimportします。

from yaf2q.f2q_mapper import F2QMapper

従来の「Jordan-Wigner変換」「Parity変換」「Bravyi-Kitaev変換」を実行するためのF2QMapperのインスタンスは、以下のように作成することができます。コンストラクタの引数として変換手法の文字列と量子ビット数を指定します。

f2q_mapper = F2QMapper(kind = "jordan-wigner", num_qubits = 4)
f2q_mapper = F2QMapper(kind = "parity", num_qubits = 4)
f2q_mapper = F2QMapper(kind = "bravyi-kitaev", num_qubits = 4)

f2q_mapperをprintすると、以下のようになります（bravyi-kitaevを指定した場合）。yaf2qでは従来の3手法を”named mapper”と呼んでいます（一般的な用語ではありません）。

print(f2q_mapper)

出力:

named mapper - bravyi-kitaev (num_qubits:4)

フェルミオン・量子ビット変換の変換行列は、encoding_matrixプロパティとして格納されています。

print(f2q_mapper.encoding_matrix)

出力:

[[1 0 0 0]
 [1 1 0 0]
 [0 0 1 0]
 [1 1 1 1]]

この変換行列は、フォック状態を量子ビット状態に変換するためのものです。例えば、|1100)というフォック状態は[1,1,0,0]というリストとして表現され、この変換行列を適用することで[1,0,0,0]というリストを得ることができ、これは量子ビット状態|1000>を表しています。この行列をフォック状態を表すリストに行列として乗算することで量子ビット状態を得ることはできるのですが、fock_to_qubit_state()というメソッドを使う方が簡単です。以下のようにします。

fock_state = [1, 1, 0, 0]
qubit_state = f2q_mapper.fock_to_qubit_state(fock_state)
print(qubit_state)

出力:

[1, 0, 0, 0]

逆変換のメソッドもあります。

qubit_state = [1, 0, 0, 0]
fock_state = f2q_mapper.qubit_to_fock_state(qubit_state)
print(fock_state)

出力:

[1, 1, 0, 0]

フェルミオン演算子を量子ビット演算子に変換する場合は、まずOpenFermionを使って解析したいフェルミオン演算子を作成することから始めます。例えば、H2分子のフェルミオン・ハミルトニアンは、OpenFermionを使って以下のように作成することができます。仕様の詳細はOpenFermionのドキュメントをご参照ください。

from openfermion import MolecularData
from openfermionpyscf import run_pyscf

molecule = MolecularData(
    geometry = [('H', (0, 0, 0)), ('H', (0, 0, 0.65))]
    basis = "sto-3g",
    multiplicity = 1
    charge = 0,
)
molecule = run_pyscf(molecule, run_scf=1, run_fci=1)
fermion_hamiltonian = molecule.get_molecular_hamiltonian()

このfermion_hamiltonian（フェルミオン演算子）をfermion_to_qubit_operator()メソッドの引数に指定することで、以下のように、量子ビット演算子を得ることができます。

qubit_hamiltonian = f2q_mapper.fermion_to_qubit_operator(fermion_hamiltonian)

このqubit_hamiltonianはyaf2qのQubitOperatorSetクラスのインスタンスになっていて、この中に、OpenFermionで定義されている量子ビット演算子クラス（QubitOperator）やqiskitで定義されている量子ビット演算子クラス（SparsePauliOp）やpytketで定義されている量子ビット演算子クラス（QubitPauliOperator）がメンバとして格納されています。各々openfermion_form、qiskit_form、およびpytket_formプロパティとして、以下のように取得することができます。

print(qubit_hamiltonian.openfermion_form)

出力:

0.03775110394645509 [] +
0.04407961290255181 [X0 Z1 X2] +
0.04407961290255181 [X0 Z1 X2 Z3] +
0.04407961290255181 [Y0 Z1 Y2] +
0.04407961290255181 [Y0 Z1 Y2 Z3] +
0.18601648886230604 [Z0] +
0.18601648886230604 [Z0 Z1] +
0.1699209784826151 [Z0 Z1 Z2] +
0.1699209784826151 [Z0 Z1 Z2 Z3] +
0.12584136558006329 [Z0 Z2] +
0.12584136558006329 [Z0 Z2 Z3] +
0.17297610130745106 [Z1] +
-0.26941693141631995 [Z1 Z2 Z3] +
0.17866777775953394 [Z1 Z3] +
-0.26941693141631995 [Z2]

print(qubit_hamiltonian.qiskit_form)

出力:

SparsePauliOp(['IIII', 'IIIZ', 'IIZI', 'IIZZ', 'IXZX', 'IYZY', 'IZII', 'IZIZ', 'IZZZ', 'ZIZI', 'ZXZX', 'ZYZY', 'ZZIZ', 'ZZZI', 'ZZZZ'],
    coeffs=[ 0.0377511 +0.j,  0.18601649+0.j,  0.1729761 +0.j,  0.18601649+0.j, 0.04407961+0.j,  0.04407961+0.j, -0.26941693+0.j,  0.12584137+0.j, 0.16992098+0.j,  0.17866778+0.j,  0.04407961+0.j,  0.04407961+0.j, 0.12584137+0.j, -0.26941693+0.j,  0.16992098+0.j])

print(qubit_hamiltonian.pytket_form)

出力:

{(Zq[0], Zq[2]): 0.125841365580063, (Zq[0], Zq[1]): 0.186016488862306, (Xq[0], Zq[1], Xq[2], Zq[3]): 0.0440796129025518, (Xq[0], Zq[1], Xq[2]): 0.0440796129025518, (Zq[0]): 0.186016488862306, (Zq[1], Zq[2], Zq[3]): -0.269416931416320, (): 0.0377511039464552, (Zq[2]): -0.269416931416320, (Zq[0], Zq[1], Zq[2], Zq[3]): 0.169920978482615, (Yq[0], Zq[1], Yq[2], Zq[3]): 0.0440796129025518, (Zq[0], Zq[2], Zq[3]): 0.125841365580063, (Zq[1], Zq[3]): 0.178667777759534, (Yq[0], Zq[1], Yq[2]): 0.0440796129025518, (Zq[0], Zq[1], Zq[2]): 0.169920978482615, (Zq[1]): 0.172976101307451}

QubitOperatorSetクラスには、固有値や固有ベクトルを求めるメソッドが定義されています。eigenvalues()メソッドの引数numに指定された数の固有値を小さいものからnum個並んだリストとして得ることができます。

qubit_hamiltonian.eigenvalues(num = 3)

同様にeigenvectors()メソッドの引数numに指定された数の固有ベクトルを固有値の小さいものからnum個並んだリストとして得ることができます。

qubit_hamiltonian.eigenvectors(num = 3)

固有値と固有ベクトルを同時に得たい場合は、eigsh()メソッドを使います。

eigenvalues, eigenvectors = qubit_hamiltonian.eigsh(num = 3)

また、パウリ重み(pauli weight)のリストを得るpauli_weights()メソッドもあります。実行すると、

print(qubit_hamiltonian.pauli_weights())

出力:

[3, 1, 4, 1, 2, 2, 3, 4, 4, 0, 3, 1, 3, 2, 3]

のようなリストが得られます。パウリ重みの平均値や最大値・最小値などを求める元データとして利用することができます。

Ternary Treeを用いた変換法

Ternary Treeは、一般には各ノードが高々3個の子ノードを持つようになっている木構造のことです。が、フェルミオン・量子ビット変換で対象としているのは、以下に示すような特別なTernary Treeです。

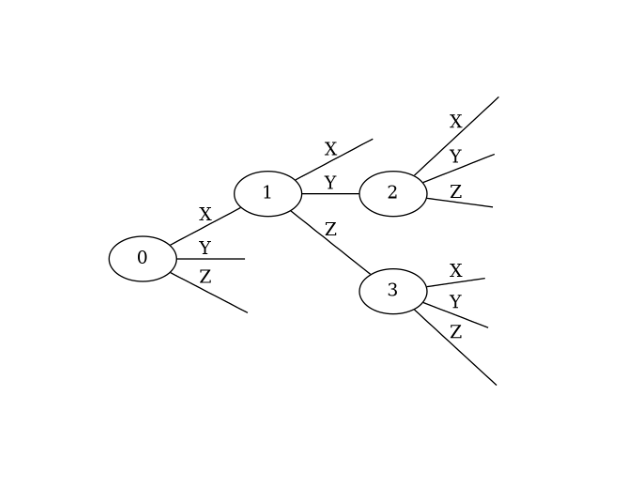
ここで、ノードは楕円で表現されておりノード番号がその中に記載されています。ノードから伸びているエッジは3本であり、各々X,Y,Zというラベルがついています。これは各々パウリX,Y,Z演算子に対応しています。一般的なTernary Treeと違うのは子ノードがないエッジも許されているということです。詳細は論文”From fermions to Qubits: A ZX-Calculus Perspective”やそれを解説したブログ記事ZX-calculusを用いたフェルミオン量子ビット変換（１）（２）（３）（４）をご参照いただくとして、ここでは、とりあえず、このようなTernary Treeによって任意のフェルミオン・量子ビット変換を規定することができて、その変換のアルゴリズムもわかっているということをおさえておけば十分です。

さて、それでは、yaf2qでどのようにこのTernary Treeを定義するかを見ていきます。それには、TernaryTreeSpecクラスを使います。そのコンストラクタに、以下のように、indicesとedgesという引数を指定することで、そのインスタンスを生成します。

from yaf2q.ternary_tree_spec import TernaryTreeSpec

ttspec = TernaryTreeSpec(
    indices = [0, 1, 2, 3],
    edges = {1: (0, 'X'), 2: (1, 'Y'), 3: (1, 'Z')},
)

ここで、indicesはノード番号のリストを表しています。4個の要素からなっているので4個のノードからなるTernary Treeということになります。edgesはエッジ集合を表しているのですが、少々説明が必要です。上の例では1,2,3をキーとして、各々に対応した値が(0, ‘X’),(1, ‘Y’),(1, ‘Z’)というタプルである辞書データとして表現されています。キーは子ノード番号を表しています。対応したタプルの1番目の要素はそれが接続している親ノード番号で、2番目の要素は、親ノードに接続するエッジのラベル文字列です。ルートノード番号は0と決められている前提です。なので、子ノードを表すキーに0は含まれません。そして、親ノード番号は必ず子ノード番号より小さく、値のタプルに重複があってはならないという前提もあります。これでTernary Treeの構造は一意に決定できます（とりあえずyaf2qで独自定義したフォーマットです）。

ttspec.show()

とすると、Ternary Tree図を表示してくれます。実は、上に図示したTernary Treeはこれで作成したものです。

Ternary Treeの木構造はこのままにして、ノード番号のみを入れ替えたものを定義したい場合もあるかもしれません。その場合は、indicesの要素の並び順のみを変えます（edgesは変えないでください）。例えば、

ttspec = TernaryTreeSpec(
    indices = [1, 0, 3, 2],
    edges = {1: (0, 'X'), 2: (1, 'Y'), 3: (1, 'Z')},
)
ttspec.show()

のようにすると、ノード番号だけ異なるTernary Treeを以下のように得ることができます（このとき、edgesは変更しないでください。変更すると木構造の形も変わってしまいます。このフォーマットについて、もう少し詳しく言うと、edgesに記載されている整数値は、いま考えているTernary Treeの最上位の親ノードから幅優先探索をしたときの探索順を表しています。別の言い方をすると、これがTernary Treeの構造を決めています。indicesはそのように順序付けられたノードのそれぞれを何番目の量子ビットとするかを表しています）。

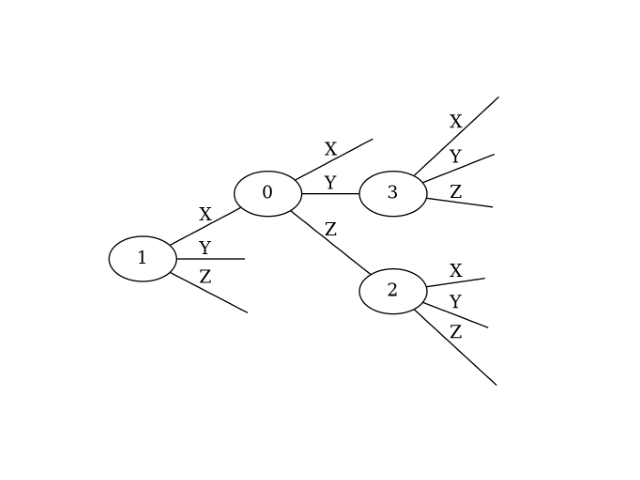
明示的にindicesとedgesを指定せずにランダムにTernary Treeを作成することもできます。以下のように、random()メソッドにノード数を引数に与えることで得ることができます。

ttspec = TernaryTreeSpec.random(4)
print(ttspec)

出力:

indices:[3, 0, 2, 1], edges:{1: (0, 'Z'), 2: (0, 'Y'), 3: (2, 'Y')

このようにTernary Treeが作成できたところで、これに基づいたフェルミオン・量子ビット変換を実行するため、以下のようにF2QMapperインスタンスを作成します。

f2q_mapper = F2QMapper(ttspec=ttspec)

これ以降は、「従来の変換法：Jordan-Wigner／Parity／Bravyi-Kitaev変換」で述べたのと同様にして、量子ビット状態を取得したり、量子ビット演算子やそれに対応した固有値・固有ベクトルやパウリ重みのリストを得ることができます。

フェルミオン・量子ビット変換の最適化

次に、フェルミオン・量子ビット変換の最適化について説明します。

いま、4個の水素原子からなる1次元水素鎖を考えて、その量子ビット・ハミルトニアンを構成するパウリ重みの平均を最小化するためのフェルミオン・量子ビット変換（＝Ternary Tree）を求めたいとします。そのために、まず、以下のように、OpenFerimionを使ってフェルミオン・ハミルトニアンfermion_hamiltonianを作成することから始めます。

from openfermion import MolecularData
from openfermionpyscf import run_pyscf

from yaf2q.ternary_tree_spec import TernaryTreeSpec
from yaf2q.f2q_mapper import F2QMapper
from yaf2q.optimizer.sa import SAParams, SA

distance = 0.65
molecule = MolecularData(
    geometry = [('H', (0, 0, 0)), ('H', (0, 0, distance)), ('H', (0, 0, 2*distance)), ('H', (0, 0, 3*distance))],
    basis = 'sto-3g',
    multiplicity = 1,
    charge = 0,
)
molecule = run_pyscf(molecule, run_scf=1, run_fci=1)
fermion_hamiltonian = molecule.get_molecular_hamiltonian()
num_qubits = fermion_hamiltonian.one_body_tensor.shape[0]

そして、TernaryTreeSpecのみを引数としてfloatを返す目的関数を以下のように定義します（関数内関数として定義してください）。

def objective_func(ttspec: TernaryTreeSpec):
    f2q_mapper = F2QMapper(ttspec=ttspec)
    qubit_hamiltonian = f2q_mapper.fermion_to_qubit_operator(fermion_hamiltonian)
    weights = qubit_hamiltonian.pauli_weights()
    weight_ave = sum(weights) / len(weights)
    return weight_ave

フェルミオン・量子ビット変換を実行してできた量子ビット演算子qubit_hamiltonianからパウリ重みリストを取得して、その平均値を返すようになっています。この目的関数は、TernaryTreeSpecを引数としてfloatを返すものであれば、どんな関数を定義しても良いです。例えば、qubit_hamiltonianに基づき量子位相推定の量子回路を作って、その回路深さを(floatとして)返すようにしても良いです。その場合、量子位相推定の深さを最小化するフェルミオン・量子ビット変換（=ternary tree）が得られます。

目的関数が定義できたら、これを最小化する解(ternary tree)を求めます。それにはyaf2qのSAクラスを使います。SAはシミュレーテッド・アニーリング(Simulated Annealing)の略です。yaf2qでは、このアルゴリズムを使って目的関数を最小化する最適解(正確には近似解)を求めるようにしています。SAのコンストラクタには、量子ビット数(num_qubit)、目的関数(objective_func)、パラメータ(params)(後述)、詳細表示するか否かを表すブーリアン(verbose)を指定します。

ttspec_opt = SA(
        num_qubits = num_qubits,
        objective_func = objective_func,
        params = SAParams(init_sampling=10, num_steps=30, cooling_factor=1.0),
        verbose = False,
).optimize()

ここで、paramsはシミュレーテッド・アニーリングを制御するパラメータSAParamsのインスタンスなのですが、これは初期サンプリング(init_sampling)、アニーリングステップ数(num_steps)、冷却因子(cooling_factor)という属性値をもっており、それらをコンストラクタで指定できるようになっています。init_samplingは初期温度を決定するためにランダムサンプリングを最初に実行するのですが、そのサンプル数です。num_stepsはアニーリングの温度を徐々に段階的に下げていく、その段階数です。cooling_factorは温度を下げていくカーブをどれだけ急峻にするかを表す因子です。0.0より大きい値を指定します。大きくなるほど急激に温度を下げる形になります。各々明示的に指定しない場合、init_sampling=10,num_steps=10,cooling_factor=1.0がデフォルト値として設定されます。どんな目的関数を定義するかによって探索の挙動は変わるので、デフォルト値で収束が悪いと感じた場合、各パラメータ値を調整する必要があります。

これで、SAによる最適化器が作成できたので、実際の最適化を実行します。すでに上に示されていますが、optimize()メソッドを使います。これにより(近似的に)最適なternary tree(ttspec_opt)が得られます。

そして、このttspec_optを使って、改めてフェルミオン・量子ビット変換を実行して、量子ビット演算子とパウリ重みを、以下のように計算して表示します。

print(f"* ternary tree:\n{ttspec_opt}")
f2q_mapper = F2QMapper(ttspec=ttspec_opt)
qubit_hamiltonian = f2q_mapper.fermion_to_qubit_operator(fermion_hamiltonian)
weights = qubit_hamiltonian.pauli_weights()
weight_ave = sum(weights) / len(weights)

print(f"* pauli weight (ave): {weight_ave}")

これを実行してみると、例えば、以下の結果を得ることができます。

出力:

[jordan-wigner]
* pauli wieght (ave): 4.583783783783784
[parity]
* pauli weight (ave): 4.691891891891892
[bravyi-kitaev]
* pauli weight (ave): 4.562162162162162
[ternary tree optimization]
* ternary tree:
indices:[3, 7, 2, 0, 5, 4, 1, 6], edges:{1: (0, 'Y'), 2: (1, 'Y'), 3: (2, 'Z'), 4: (3, 'Z'), 5: (4, 'Y'), 6: (3, 'X'), 7: (4, 'X')
* pauli product length (ave): 4.4324324324324325

従来の3手法と比べ、最適Ternary Treeのパウリ重みが一番小さいという結果になっています。

シミュレーテッド・アニーリングは確率的な手法なので、実行のたびに[ternary tree optimization]の結果は変わります。が、乱数のシードを固定することで、結果を固定することもできます。以下のようにseedを指定します。

ttspec_opt = SA(
        num_qubits = num_qubits,
        objective_func = objective_func,
        params = SAParams(init_sampling=10, num_steps=30, cooling_factor=1.0, seed=123),
        verbose = False,
).optimize()

以上